Brechung und Beugung

Ganz oft werden die beiden optischen Phänomene Brechung und Beugung verwechselt.

 

Brechung:

In der geometrischen Optik kennt man den Begriff des Lichtstrahles. Er zeigt längs einer Linie die Ausbreitung von Licht an.
Lichtstrahlen gehen immer gerade aus, sie können weder an Brechung noch an Beugung beteiligt sein. Brechung und Beugung beschreiben die Abweichung vom gradlinigen Fortschreiten des Lichtes.

Nach einem gängigen Modell wird die Brechung als Bremsvorgang eines Lichtbündels beschrieben:

Brechung tritt immer auf, wenn Licht von einem Medium (z.B. Luft) in ein anderes wechselt (z.B. Glas).
Damit Brechung beobachtbar wird, darf aber nicht ein einzelner unendlich dünner Lichtstrahl sondern muss ein ganzes breites Bündel von Licht auf ein anderes Medium treffen. Dann wird es abgelenkt.
Wir alle wissen: Beim Übergang von Luft in Glas wird Licht zum Einfallslot hin gebrochen.

Die Ablenkung tritt auch nur ein, wenn das Lichtbündel nicht senkrecht auftrifft.
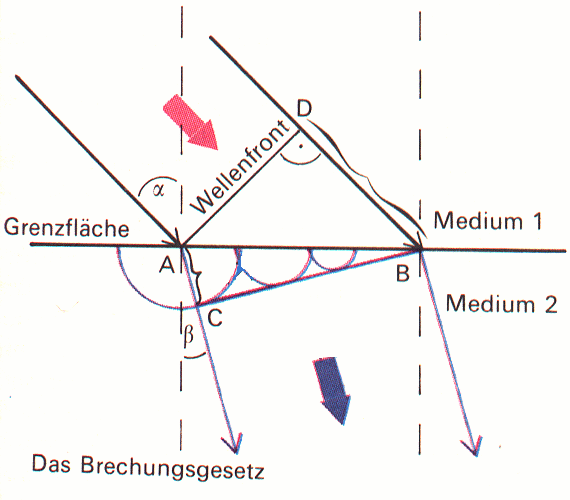
Die Ursache der Ablenkung ist nämlich (beim Übergang von Luft in Glas) die Abbremsung. Der Teil des Lichtbündels (bzw. der Wellenfront), der zuerst in das andere Medium eindringt, wird langsamer, der andere Teil läuft ungehindert weiter.
Dadurch knickt das Lichtbündel ab.

Physikerboard

Das ist wie bei einem Auto, das in den rechten Seitenstreifen gerät. Die rechten Räder werden abgebremst und der Wagen verliert die Spur, er bewegt sich nach rechts, verlässt die Straße.
Ein einzelner Lichtstrahl kann als unendlich dünn angesehen werden, der kann somit nicht gebrochen werden, weil nicht Teile von ihm abgebremst werden können.
Man braucht also einen breiten Lichtstrahl, um beim Übergang den Bremseffekt zu spüren und damit die Ablenkung, also ein Lichtbündel.

Und da sind wir auch schon beim ersten Merkspruch:

Man muss breit sein, um zu brechen....

Dürften leider einige kennen...Ausnahme: Man hat was Falsches gegessen...

Aus den maxwellschen Gleichungen erhalten wir eine Formel für die Lichtgeschwindigkeit in Medien. Dabei  ergibt sich:

Je leichter die Ladungen verschiebbar sind, desto stärker wird Licht abgebremst.

 

 Schon in der Antike war bekannt, dass das Brechungsgesetz durch eine Optimierung des Weges erklärt werden kann. Dabei kommt es nicht auf den geometrischen Weg an, sondern auf den Weg mit der geringsten Wirkung, also den Weg, den ein Lichtstrahl in der kürzesten Zeit zurück legt.
 

Das hat Fermat schon 1650 erkannt, und deshalb nennt man das auch das Fermatsche Prinzip.

Zur Veranschaulichung wird oft das folgende Beispiel verwendet:

 

Ein Rettungsschwimmer A am Strand sieht einen Ertrinkenden C im Wasser. Am Strand kann er recht schnell laufen, ist aber beim Schwimmen im Wasser deutlich langsamer.
Wählt er den direkten Weg (1) ist er zu lange im Wasser, er braucht zu viel Zeit.
Der Weg (2) hat zwar die kürzeste Schwimmstrecke, aber dafür wird der Weg am Strand zu lang.

Am schnellsten ist der Rettungsschwimmer, wenn er bei B ins Wasser tritt, also genau so läuft wie das Brechungsgesetz es vorschreibt.
Im Wasser ist Licht langsamer, die  Geschwindigkeit sinkt auf c/n. Dabei ist c die Lichtgeschwindigkeit in Luft (fast so wie im Vakuum) und n der Bremsfaktor, den man auch Brechungsindex nennt.
Wir vernachlässigen hier die leichte Abbremsung von Licht in Luft.
Das Licht wählt nach Fermat den Weg mit der kürzesten Laufzeit.

Mathematisch ist das eine Extremwertaufgabe, die man in der Q2 leicht lösen kann:
Man sucht die Lage von B, bei der die gesamte Laufzeit minimal wird.
Heraus kommt das Brechungsgesetz!

Für den Übergang Luft nach Glas/Wasser lautet das Gesetz vereinfacht:

sin α /sin β = n

Uni Wien

Selbst Feynman hat die Frage gestellt: "Woher weiß denn das Licht, welchen Weg es gehen muss? Es geht nur von A nach C, wie vergleicht es andere Wege und findet den optimierten?"

 

 

Es gibt mehrere Wege in der klassischen Mechanik die Bewegungsgesetze zu finden:
Newton beschreibt die Bewegungen durch den Impuls, den Schwung, der Körper. Es gibt das Prinzip der Impulserhaltung, das Newton in seinen drei Axiomen jeweils unterschiedlich formuliert hat (Trägheitsgesetz, F = m*a und actio= reactio).

Leibniz beschreibt Bewegungen durch die Energien, die die Körper haben und nutzt den Energieerhaltungssatz.

 Unter der Wirkung einer Bewegung versteht man die Summe aus den Differenzen von kinetischer Energie und potenzieller Energie, an jedem Punkt der Bahn aufaddiert.
Das Prinzip der kleinsten Wirkung besagt, dass diejenige Bahn in der Realität vorkommt, bei der diese Summe am kleinst möglichsten ist.

Das ist vollkommen äquivalent zu der Formulierung von Fermat, dass Licht immer den schnellsten Weg wählt um von A nach C zu kommen.

In einem der bekanntesten Lehrbücher der Physik (Gehrtsen) steht dazu:
"Die Welle probiert ständig alternative Wege aus und schickt Elementarwellen auf diese, aber auf allen Irrwegen interferieren sich diese Elementarwellen weg, nur auf dem richtigen Weg verstärken sie sich."

Aus diesem Wirkungsprinzip lassen sich die Langrangeschen Bewegungsgleichungen herleiten, die so universell sind, dass man damit auch in der Quantenmechanik, der Quantenfeldtheorie und der Relativitätstheorie arbeiten kann.

Nun könnte man denken, dass diese "Irrwege" nicht wichtig sind und dass man sie auch ausblenden könne. Falsch gedacht...macht man das, dann weichen Lichtstrahlen von ihren gradlinigen Wegen ab und es entsteht Beugung. Die Irrwege sind also kein Rechentrick, sondern werden wirklich durchlaufen.

Zitieren wir noch einmal Feynman:
"Riecht es (..das Licht...) die nahe gelegenen Wege und vergleicht diese miteinander? Die Antwort ist: Ja, das tut es,...sozusagen..."
Was er damit meint, wird mit seiner berühmten Pfadintegralmethode deutlich:
"Licht muss nicht wissen, welchen Weg es gehen soll...es geht alle möglichen Wege. Nur Wege nahe dem mit dem kleinsten Zeitaufwand haben Phasenpfeile, die nahezu parallel zueinander liegen und zur hohen Wahrscheinlichkeit dafür beitragen, dass dieser Weg genommen wird." (bzw. sich die anderen auslöschen...)

 

 In dem norwegischen Lehrbuch über Wellen ( Kurland, Vistnes:  Physics of Oscillations and Waves. 2018) habe ich folgende schöne Zusammenfassung gefunden:

The waves follow all possible ways, but in some cases the waves reinforce each other, and in other cases, they will oppose each other. In other words, it is interference that is actually running the show, and the central idea behind this phenomenon is the role played by the relative phases of the different contributions. The “minimum time” criterion achieves the desired result automatically, since minimum time means that many waves, which we can imagine to have been sent from P , will take close to the minimum travel time and all these waves will automatically have the same phase and therefore interfere constructively.

Wir haben jetzt verschiedene Vorstellungen als Modell von Brechung entwickelt. Wir müssen ja Brechung von Beugung abgrenzen: Im Prinzip geht das jetzt schon:
Brechung findet nur statt, wenn alle möglichen Wege zur Verfügung stehen.  Schränkt man die möglichen Wege ein, so entsteht ein anderes Phänomen, die Beugung.

Aber bevor wir zur Beugung kommen, noch etwas mehr zur Abbremsung von Licht:

Wir haben verschiedene Modelle kennengelernt, die Brechung von Licht zu erklären:
das Fermatsche Prinzip der kürzesten Laufzeit, das Prinzip der kleinsten Wirkung und das Huygensche Prinzip, das die Abbremsung eines breiten Lichtbündels heranzieht.

Und genau um diese Abbremsung soll es gehen, denn die kann man wirklich direkt messen. Licht ist in Glas langsamer als im Vakuum.

Aber das ist kein echtes Abbremsen, sondern nur "ein Schwätzchen mit den Atomen halten"

Licht wird in Glas von Atom zu Atom geleitet. Ein Atom braucht aber immer einen winzigen Bruchteil einer Sekunde (etwa eine hundertmillionste Sekunde) zwischen Aufnahme und Weitergabe. Und während ein Lichtstrahl durch Glas geht, trifft er auf Millionen von Atomen...

Für die 50 km Autobahnstrecke zwischen Kassel und Göttingen brauche ich eine halbe Stunde, wenn ich immer mit 100 km/h fahre....wenn ich aber drei Pinkelpausen auf Parkplätzen einlege, brauche ich länger...und wenn ich dann die 50 km durch die Fahrzeit teile, komme ich auf eine kleinere Geschwindigkeit...obwohl ich immer 100 km/h gefahren bin, wenn ich denn gefahren bin.

Also: Licht wird in Glas nicht langsamer, es trödelt nur bei den Zwischenstopps rum...

Das kann man etwas genauer mit Hilfe von erzwungenen Schwingungen beaschreiben:

In diesem Modell betrachten wir Atome als Oszillatoren, die von der ankommenden Lichtwelle zum Schwingen angeregt werden.
In der Physik ist das eine sog. erzwungene Schwingung:
Ein Pendel (der Erreger) überträgt seine Schwingung auf ein zweites Pendel, den Resonator.

Der Resonator hat eine ihm eigene Frequenz f₀, Ist die Frequenz des Erregers f_E  genau so groß, so liegt der Resonanzfall vor: die Schwingung wird schnell und optimal weitergegeben.

Der Lichtstrahl würde dann fast vollständig absorbiert werden und die Abbremsung ist minimal, der  Brechungsindex n fast genau 1.

Liegt die Lichtfrequenz deutlich unter der Resonanzfrequenz der Atome, so wird wenig Licht absorbiert und der Brechungsindex steigt mit der Frequenz an: Blaues Licht wird stärker gebrochen wie rotes Licht.

In unmittelbarer Umgebung kommt es zu einem Abfall des Brechungsindex mit steigender Frequenz: kurzwellige Strahlung wird dann schwächer gebrochen. Dies ist die anomale Brechung.
Bei fast allen Materialien ist die Resonanzfrequenz bei Wellenlängen im UV, wir haben also im sichtbaren Licht normale Brechung vorliegen.

Ich habe das mal als Skizze dargestellt. Man erkennt das beschriebene Verhalten des Brechungsinsdex n und in blau unterlegt die passende Absorptionskurve.

 

Die Brechung hängt also von der Wellenlänge des Lichtes ab, das nennt man auch Dispersion.

Brechung und Absorption hängen zusammen. Das drückt man durch den gemeinsamen komplexen Brechungsindex N aus.

Es gilt N² =(n -i*a)², dabei ist der Realteil n der normale Brechungsindex und a die komplexe Absorption (durch die Multiplikation mit i = √(-1) entsteht beim Ausrechnen eine reelle Zahl, der Absorptionsgrad),

Online Kurs über komplexe Zahlen

Fazit: Das Abbremsen des Lichtes bei der Brechung kommt durch die nicht resonante Anregung der Atome durch den Lichtstrahl und die dadurch verzögerte Weitergabe des Lichtes.

Beugung:

Auch bei der Beugung verlässt  das Licht den  geraden Weg eines Lichtstrahles.
Bei der Brechung passiert dies, weil in einem anderen Medium Wege und Wirkungen optimiert werden bzw. ein Teil des Lichtbündels beim Übergang zuerst abgebremst wird (je nach Modell mit dem man das verstehen will).

Auch bei der Beugung muss es ein anderes Medium geben. Aber in dieses dringt das Licht nicht ein, es regt nur Atome am Rand des anderen Mediums an eigene, kugelförmige, Lichtwellen abzustrahlen.
Diese Wellen, Huygens hat das etwas komplizierter als Elementarwelle konstruiert, dringen dann auch in Bereiche ein, die eigentlich als Schattenbereiche dunkel bleiben sollten.
Das nennt man Beugung.
Ganz oft überlagern sich dann auch viele dieser Wellen, es tritt Interferenz auf, also ein Beugungs- und Interferenzmuster aus hellen und dunklen Bereichen.


Beugung ist eine wirklich typische Wellenerscheinung.
Beugung tritt also auch auf bei den Wahrscheinlichkeitswellen der Quantenmechanik, bei Schallwellen, Wasserwellen, Erdbebenwellen und natürlich Licht und Radiowellen.

Kurzwelliges Licht wird zwar stärker gebrochen (siehe der frühere Merkspruch), aber weniger stark gebeugt. Je kurzwelliger eine Strahlung ist, desto schwieriger ist es sie "vom Weg abzubringen".
Bei der extrem kurzwelligen Röntgenstrahlung hat es Jahre gebraucht um ihre Welleneigenschaften durch Beugung zu entdecken.

Beugung von Wasserwellen, University of Louisville

Lange Wellenlängen können bevorzugt in Schattenräume eindringen.

Dazu gibt es zwei Beispiele:

Wenn eine Musikkapelle bei einer Kirmes hinter einer Straßenecke spielt, hört man zuerst die tiefen, langwelligen Töne "um die Ecke kommen". Das Piepsen der Flöten hört man erst, wenn man die Spieler/innen auch sieht...
Wenn bei einem Mondhof das Mondlicht an feinen Wassertröpfchen gebeugt wird, führt das dazu, dass der innere Teil des Hofes aus wenig gebeugtem blauen Licht und der äußere Bereich aus stärker gebeugtem roten Licht besteht.

Beugung an der Fernrohröffnung:

Jede Person, die durch ein Fenrrohr sieht, kann selbst Beugungserscheinungen beobachten.
Bei einem Linsenfernrohr wird das Sternenlicht an der Fassung der Linse gebeugt, bei einem Spiegelteleskop noch deutlicher am Fangspiegel.

Um diese Beugungserscheinungen zu sehen (die gebeugten Wellen erzeugen ein streifenförmiges Intereferenzmuster aus hellen und dunklen Streifen um das Beugungsobjekt herum), muss man lediglich das Bild unscharf stellen.

Man kann Unschärfe erreichen, wenn man das Okular weiter nach Außen (extrafokal)  oder weiter nach Innen (intrafokal) dreht. Je nach Spiegelart (Kugelspiegel, Parabolspiegel) und Justierung unterscheiden sich die Beugungsbilder deutlich.

Mit Hilfe solcher Beugungsbilder habe ich oft Spiegelteleskope justiert.

Aber die Beugung des Lichtes hat auch Nachteile: Wir sehen keinen Lichtpunkt als Stern, sondern einen kleinen Kreis (0.Interferenzmaximum), umgeben von schmalen helleren Ringen.
Steht nun ein zweiter Stern dicht daneben, erzeugt er ebenfalls so ein Ringsystem. Beide Sterne können wir nur getrennt wahrnehmen, wenn die helleren 0. Maxima deutlich nebeneinander liegen.
Beugung begrenzt also das Auflösungsvermögen der optischen Geräte.

Bild: Teleskopservice

Bilder und Text stammen aus einer Postserie, die im Juni und Juli 2020 in meinem Blog über Astronomie veröffentlicht wurden:

Astronomie-Blog