Auflösungsvermögen

Das Auflösungsvermögen:

Begriffsbildung

Prinzipiell unterscheidet man zwei Bereiche, bei denen die Auflösung eine Rolle spielt:

a) Spektrale Auflösung:

Man möchte in Spektren verschiedene Wellenlängen deutlich getrennt untersuchen können. Beispielsweise könnten zwei Komponenten einer Spektrallinie durch Magnetfelder entstehen und die Untersuchung würde etwas über das Magnetfeld aussagen.
Bezeichnet man mit Δλ den Abstand zweier noch trennbarer Wellenlängen, dann wird mit  λ/Δλ das Auflösungsvermögen A bezeichnet.
Ein Spektrum mit einem Auflösungsvermögen A = 200 000 kann also bei einer  Wellenlänge von 500 nm noch Abstände von 500nm /200000 = 0.0025 nm trennen.
Mit dem spektralen Auflösungsvermögen wollen wir uns jetzt nicht näher nicht beschäftigen, es kommt aber im Sinne der obigen kleinen Rechnung durchaus in Abituraufgaben vor.. 

Wir wollen nun  zeigen: Für ein Gitter mit N beleuchteten (!) Öffnungen ist das Auflösungsvermögen im Spektrum der Ordnung n gleich n * N: 

A = n*N

 Die beiden Wellenlängen λ und λ+ Δλ  ( die sich also um Δλ unterscheiden), können noch getrennt gesehen werden, wenn das n.-te Maximum der längeren Wellenlänge λ  + Δλ mit dem nächsten Nebenminimum von λ zusammenfällt.

In Formeln übersetzt heißt das:

 Gleichsetzen der sinus-Werte der Richtungswinkel dazu:

n.tes Maximum der längeren Wellenlänge im  (n*N + 1).ten Nebenminimum

  n*(λ + Δλ) /g    =     (n*N + 1) * λ  / (N+g)

   g kann man auf beiden Seiten "kürzen", rechts N ausklammern und ebenfalls kürzen

dann erhält man:

n*λ + n* Δλ  = n* λ + 1/N* λ

daraus:  n* Δλ  = 1/N* λ

und schließlich für das Auflösungsvermögen eines Gitters:

    A =  λ / Δλ = n* N

 Die Minima-Formel für Gitter muss man im Abi nicht können....aber wenn man die Aufgabe für einen Doppelspalt (N=2) stellt, kann man mit offiziell bekannten Formeln für Maxima und Minima beim Doppelspalt genau so vorgehen...das kommt öfters vor.

b) Winkelauflösung

Man möchte am Himmel noch Sterne getrennt sehen, obwohl sie sehr dicht beieinander stehen. Ein Fernrohr erhöht bekanntlicherweise das Auflösungsvermögen.
Für zwei  punktförmige Objekte (Sterne) ist der kleinste Winkelabstand, unter dem man sie am Himmel noch sehen kann:

α = 1,22*λ/D

Dabei wird  α im Bogenmaß angegeben, λ ist die Wellenlänge, bei der man beobachtet, und D der Durchmesser des Teleskops.
Achtung:  λ und D müssen  in der gleichen Einheit angegeben werden.

Zum Bogenmaß: 360° entsprechen 2*π, 1" (1/3600 eines Grades) sind dann 0,00000485 im Bogenmaß.

Was bedeutet diese Formel ganz praktisch:

Je größer der Durchmesser D des  Fernrohrs, desto kleinere Winkelabstände kann man trennen. Und die Auflösung steigt, wenn man kurzwelliges Licht benutzt (siehe Bild von astroshop.de)

 Nehmen wir ein Beispiel:

Unser Auge hat für sichtbares Licht (bei 550 nm) etwa eine Auflösung von 1`. Wir können  also den 60.-ten Teil eines Grades wahrnehmen. Der Mond hat einen Winkeldurchmesser von 30`, wir sehen also Mare und sehr große Krater mit dem freien Auge. Mizar und Alkor im Großen Wagen haben einen Winkelabstand von 12´, sie wären also leicht getrennt wahrnehmbar, wenn der Helligkeitsunterschied nicht so groß wäre. Erst deshalb nennt man sie auch Augenprüfer.

Ein kleines Teleskop mit einem Durchmesser von 11 cm hat ein Auflösungsvermögen von 1", das entspricht etwa dem mittleren Wackeln durch die Luftunruhe..., dem sog. Seeing.
Fernrohre mit größerem Durchmesser machen also auf der Erdoberfläche eigentlich wenig Sinn, oder?

Das Rayleigh-Kriterium

Fernrohre sollen natürlich nicht nur eng beieinanderstehende Objekte getrennt aufnehmen, sondern auch viel Licht sammeln um auch lichtschwache Himmelskörper nachzuweisen.
Insofern ist es schon sinnvoll, größere Fernrohre als mit 11 cm Durchmesser zu bauen...

Und man achtet natürlich auch auf den richtigen Standort mit möglichst gutem Seeing, d.h. geringer Luftunruhe. Das sind in der Regel Berggipel, möglichst über Wüsten oder bei Sonnenteleskopen Sternwarte von Wasser umgeben oder gar Fernrohre auf Satelliten außerhalb der Erdatmosphäre.
Und es gibt natürlich inzwischen Tricks die Luftunruhe auszuschalten...dazu aber später mehr.

Wodurch entsteht das begrenzte Auflösungsvermögen eines Fernrohres?

Die Ursache ist letztlich die wellenförmige Ausbreitung des Lichtes. Jede Fernrohrlinse oder jeder Spiegel hat einen Rand und vom Rand gehen Lichtwellen aus, die auch nach Innen strahlen (sog. Elementarwellen) und dabei Interferenzen erzeugen.

Die Wellen können sich so überlagern, dass sie sich verstärken, dann spricht man von Interferenzmaxima. Löschen sie sich dagegen aus (ein Wellenberg trifft auf ein Wellental), dann gibt es ein dunkles Interferenzminimum.
Alle Interferenzmaxima besitzen eine bestimmte Ausdehnung.

Wer ein Fernrohr hat, kann sich das leicht ansehen. Man stelle einen hellen Stern ein und stelle das Bild unscharf. Dann erschient ein heller zentraler Lichtfleck (das 0. Maximum, das Beugungsscheibchen) und drumherum abwechselnd helle und dunkle Ringe.
Das sind die Interferenzen des an der Fernrohrfassung gebeugten Lichtes.

Also: Fernrohre erzeugen keine punktförmigen Sternbilder sondern lediglich Beugungsscheibchen. Die sind um so kleiner, je größer das Fernrohr und je kürzer die Wellenlänge sind.

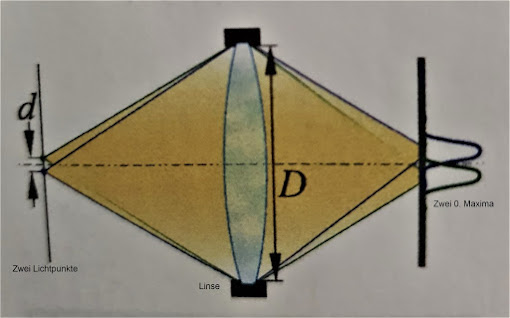
Wenn man nun zwei dicht nebeneinander stehende Sterne ansieht, erzeugt das Fernrohr also keine Lichtpunkte, sondern Interferenzsysteme aus einem dicken 0. Maximum und weiteren ringförmigen Maxima. Und zwar für jeden Stern getrennt und versetzt.
Fallen die beiden dicken 0. Maxima der beiden Sterne zu sehr aufeinander, dann können wir sie nicht mehr getrennt sehen (Bild aus Roth/Stahl, Optik, 2020). Wir können auch sagen, die beiden Beugungsscheibchen müssen weit genug voneinander getrennt sein, damit ich die beiden Sterne einzeln erkennen kann.

 

Rayleigh hat ein recht willkürliches Kriterium aufgestellt: Fällt das 0. Maximum des einen Sternes in das erste Minimum des anderen Sternes, so kann man die beiden Sterne noch garantiert getrennt sehen.

 Wir kennen die Formel für das erste Minimum am Spalt. Es liegt bei einem Winkel α, für den gilt:

sin α = λ/D  (λ Wellenlänge, D Spaltdurchmesser).

Ein Spalt ist ein rechteckförmiges Beugungsobjekt, Fernrohre sind rund... da muss  man mit den sog. Besselfunktionen arbeiten und erhält sin α = 1,22 * λ/D.
Für die kleinen Winkel kann man den Sinus auch weglassen und den Winkel  α   durch das Bogenmaß ersetzen.

Mit dieser berühmten Formal kann man alle Werte ausrechnen, die ich im letzten Post genannt habe.

Im neuen Optiklehrbuch von Roth und Stahl sind einige sehr schöne Darstellungen zum Thema zu sehen: Von Bild A über B zu C werden zwei Lichtpunkte immer besser aufgelöst, das mittlere Bild entspricht ungefähr der von Rayleigh gesetzten Grenze.

 Das menschliche Auge

Wir haben die Formel α = 1,22*λ/D für den kleinsten Winkel α (im Bogenmaß) kennengelernt, die man mit einem optischen Gerät des Durchmessers D bei der Wellenlänge λ noch trennen kann.
Grundlage der Formel ist die Beugungstheorie, nach der die Abbildungen der Sterne keine Punkte sondern kleine Beugungsscheibchen sind, die man noch nebeneinander getrennt sehen können muss, will man zwei Objekte getrennt wahrnehmen.

Wenn man Objekte getrennt wahrnehmen will, muss aber auch der Aufbau des Detektors sinnvoll sein:
Wird das Objekt mit seiner gesamten Struktur auf einen einzigen Pixel einer CCD-Schicht abgebildet oder auf eine einzige Sinneszelle im Auge, so kann man natürlich keine innere Struktur des Objektes wahrnehmen.

Der Abstand der lichtempfindlichen Zellen im Auge muss also z.B. an das Auflösungsvermögen des Linsensystems angepasst sein.

Bei Fernrohren und CCD-Chips machen das die Techniker, bei unserem Auge die Evolution:

Nehmen wir eine Wellenlänge von 500 nm (hier ist die Sonne am hellsten und unser Auge am empfindlichsten). Bei einem Durchmesser von 5 mm lässt sich nun der kleinste Winkel ausrechnen. Bei einem entspannten Auge entsteht das Bild 22 mm hinter der Linsenmitte (Brennweite). Damit können wir den Winkel umrechnen und erhalten einen minimalen Abstand auf der Netzhaut von 2,5 μm.
Die Sinneszellen auf der Netzhaut liegen ungefähr 3 μm voneinander entfernt.

Gut angepasst!

Wer das mal ausprobieren will: Aus einem Abstand von 1 m kann man noch zwei Punkte getrennt wahrnehmen, die 0,15 mm voneinander entfernt sind.

Bilder: Medizin kompakt, ETH Zürich

 

Übungsaufgabe:

Pointillismus ist eine besondere Stilrichtung der Malerei zwischen 1889 und 1910.
Kleine Farbpunkte wurden im Abstand von etwa 2 mm auf die Leinwand gemalt.
Als Beispiel seht ihr hier das punktierte Gemälde "Das Frühstück" von Paul Signac, das 1886/87 entstanden ist.

Das eigentliche Bild entsteht erst durch die Begrenzung des Auflösungsvermögens des Auges, also durch Beugung an der Pupillenöffnung des Betrachters.

In welchem Abstand sollte sich eine Person befinden, damit sie alle (!) Farben zu einem Bild gemischt sieht? Der Pupillendurchmesser soll als 5 mm angenommen werden.
Was ändert sich, wenn das Bild mit einem hellen Scheinwerfer bestrahlt wird?

Lösung:

Zuerst muss man die Formel für das Auflösungsvermögen nehmen:
Der kleinste noch trennbare Winkelunterschied ist 1,22* λ/D, wobei D hier der Pupillendurchmesser ist.
Für kleine Winkel kann man dafür d/E schreiben, dabei ist d der Abstand der Punkte und E die Entfernung des Betrachters.
Setzt man das gleich und löst nach E auf, so erhält man:

E = d*D/(1,22*λ)

Da die Auflösung  für kurzwelliges Licht am schwächsten ist, sollte man für  λ = 400 nm einsetzen. d ist der Abstand der Punkte, also 2 mm. Bei schwacher Auflösung  ist ja das Zerfließen der Punkte in einander am stärksten
Dann erhält man einen Mindestabstand von 20 m.

Wir das Bild hell angeleuchtet, verkleinern sich die Pupillen unserer Augen (D nimmt ab, vielleicht auf 3 mm), die Auflösung wird schwächer und man kann näher rangehen und sieht trotzdem die Punkte überlagert.

Weiterführendes:

Das Seeing überlisten

Das Auflösungsvermögen der Fernrohre wird durch die Luftunruhe (seeing) begrenzt, so dass es sich kaum lohnt größere Fernrohre als mit 11 cm Durchmesser zu bauen...
Aber bei extrem guten Wetterlagen, in bestimmten Umgebungen und in größerer Höhe ist das Seeing besser.
Und außerhalb der Atmosphäre, beim Hubble Space Teleksop z.B. stört es logischerweise nicht...

Vor etwa 20 Jahren begannen Astronomen eine Technik von den Militärs zu übernehmen, mit denen lange Zeit hochauflösende Spionagebilder von Satelliten aus gemacht wurden:  adaptive Optik.

Die Idee klingt einfach, aber erst moderne und schnelle Computer ermöglichen die vielfältige Anwendung:

An einem Stern oder einem durch einen Laserstrahl angeregtes künstliches Leuchten in großer Höhe testet man die momentane Auswirkung der Luft auf die Bilder, bis zu 1000 mal in der Sekunde.
Ein schneller Computer rechnet aus, wie das ankommende Licht so verändert werden muss, dass in diesem Moment die Störung der Luft aufgehoben wird.
Das vom Fernrohr aufgenommene Licht wird vor der Untersuchung im Detektor deshalb auf einen kleineren dünnen Spiegel gelenkt, der vom Computer so verformt wird, dass er die Verformung des Lichtbündels durch die Luft in diesem Moment aufhebt.
Die adaptive Optik ist nicht mit aktiver Optik zu verwechseln. Bei der aktiven Optik wird lediglich die Parabolform des Spiegels aktiv korrigiert.

Durch die adaptive Optik  erhält man gestochen scharfe Bilder und man kann die Wirkung der Lufthülle in Echtzeit ausschalten.
Erst jetzt macht es auch Sinn Interferometrie zu betreiben.

Bilder: ESO (Uranus mit und ohne adaptive Optik, Funktionsschema)

Große Fernrohre simulieren

Das Auflösungsvermögen ist durch den Durchmesser eines Fernrohres bestimmt. Große Fernrohre zu bauen ist sehr aufwändig und vor allem sehr teuer. Das neue 39 m Teleskop ist ein Jahrhundertprojekt.
Viel einfacher ist es ein großes Fernrohr dadurch zu simulieren, dass man kleinere Fernrohre zusammenschaltet.

Mit Radioteleskopen macht man das schon seit Jahrzehnten: Radiostrahlung kann man speichern und anschließend die Radiostrahlung, die verschiedene Radioteleskope zur gleichen Zeit vom gleichen Objekt aufgenommen haben, überlagern.
Aus diesen Überlagerungen kann man dann mit hoher Auflösung das Radiobild konstruieren.
Das nennt man VLBI: Very Long Baseline Interferometrie. Dabei können die Radioteleskope durchaus auf verschiedenen Kontinenten stehen. Ein Computer verschiebt die Signale so gegeneinander, bis sie passen und die Interferenzstruktur entsteht.

Auf ähnliche Weise hat man mit Mikrowellen  beim Event Horizon Teleskop die erste Aufnahme der unmittelbaren Umgebung eines Schwarzen Loches gewonnen.

Lichtwellen kann man nicht direkt als Welle speichern, deswegen müssen die Interferenzen hier live vorgenommen werden. Das gelang erstmalig vor etwa 20 Jahren beim VLTI, also Jahrzehnte nach den Radiointerferometern.

Teilstandorte des EHT (University of Arizona)

Das erste Bild der Umgebung eines supermassiven Schwarzen Loches im Zentrum einer Galaxie

Prinzip der modernen VLB-Interferometrie (NASA)

 

 Wie  schon gesagt, können Lichtwellen nur live verarbeitet werden. Will man mit mehreren Fernrohren ein großes simulieren, dann muss man das von den Teleskopen empfangene Licht sofort zur Überlagerung bringen und das Interferenzmuster ausmessen.

Inzwischen funktioniert diese Technik sogar mit 4 Teleskopen.
Beim VLT in Chile kann man die vier großen Teleskope zusammenschalten, aber auch die vier kleinen beweglichen Teleskope.

Durch die Beweglichkeit kann man die Auflösung noch erhöhen, man simuliert ein Teleskop mit etwa 200 m Durchmesser.

Seit 2015 ist ein neues Interferometer beim VLT in Betrieb, Gravity genannt. Damit konnte man einen erheblichen Beitrag zur Strukturuntersuchung der Umgebung Schwarzer Löcher leisten.

Die Grundidee eines Interferometers ist die folgende: Man fährt den Himmel mit allen angeschlossenen Teleskopen ab, bringt ihr Licht zur Überlagerung und registriert, aus welcher Richtung die höchste Intensität (das 0. Maximum) kommt.

Damit das funktioniert, darf kein zusätzlicher Gangunterschied durch den Transport des Lichtes von den Fernrohren zum Interferometer entstehen.
Deswegen wird beim VLT-I das Licht durch den Interferometertunnel geleitet. Hier kann man unterschiedliche Weglängen mit Nanometer-Genauigkeit ausgleichen, einmal grob, in dem ein Spiegelwagen verschoben wird und einmal fein, in dem die Spiegel durch Piezokristalle innerhalb des Wagens verschoben werden.

Als ich 2013 zu Gast beim VLT in Chile war, durfte ich durch eine besondere Genehmigung des ESO-Chefs in den Interferometertunnel hinein.
Das System ist so empfindlich, dass erst am nächsten Tag wieder nach einer Neujustierung damit gearbeitet werden konnte. Aber in der Nacht nach  meinem Besuch war der Einsatz nicht vorgesehen.
Jahrzehntelang musste man mit Radioteleskopen Interferometrie betreiben, wenn man Details der astronomischen Objekte erkennen wollte, obwohl ein einzelnes Radioteleskop wegen der langen Wellenlänge ein schlechteres Auflösungsvermögen als das menschliche Auge hat.
Dank des VLT-I in Paranal können die optischen Astronomen jetzt ebenfalls direkt die Struktur der Objekte ansehen und im Bereich von Mikrobogensekunden messen.

Bilder:
- Lichtwege im Interferometertunnel (ESO)

- Im Interferometertunnel (eigene Aufnahme)

- Spiegelwagen (eigene Aufnahme)

 

Zusammengestellt aus einer Postserie meines Astronomie-Blogs:

Astronomie-Blog